ПАМЯТИ
КЛОДА ШЕННОНА
Сережа, видишь ли.
Не знаю, с чего начать...
Начну с чего-нибудь, расскажу
о том, что было после того,
как я не дождался тебя у метро
и ушел один по бульварам гулять.
Летняя полночь в Париже.
И я,
не глядящий дальше письменного стола,
мышки, клавиатуры, экрана,
сосредоточенный на кончике карандаша,
я должен был видеть вулканы
открытых, кипящих, ночных кафе.
Хорошо. Стараясь как можно ровней дышать,
я за сорок минут дошел до Марэ
и вошел наугад в пещеру чудовищ,
где провел в общей сложности полтора часа.
Что меня привело туда,
кроме желания встряхнуть нервы,
возбудить невидящие глаза?
Предупреждаю крик.
Твой - что ты со всем арсеналом
эстетики, этики, только что не дианетики,
подвергнешь ужасающей критике
мой визит в пещеру цветных огней,
ритмичной музыки, негритянского пения,
чрезмерного, возможно, употребления
спиртных напитков, сигарет курения,
нецеломудренного поведения,
и меня заклеймишь за пребывание в ней.
Я мог тебе ничего и не говорить.
А пятьдесят франков - сказать, что попросту дал кому-то
или где-нибудь потерял.
Но послушай меня.
Есть простые истины, например вот эта:
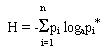
и по ней - ты требуешь у действительности ответа
на вопрос о грозящей тебе опасности
и ты имеешь право такой ответ получить.
Наученный горьким белым мартини,
я смотрел, как пляшут цветные тени
и тени черные, которые отбрасывали на стены
все явления там, и старался предугадать
конфигурацию следующей картины.
Что же такое пророчество? Ты помнишь, Сережа, мои стихи
про лейтенанта Смита, сбитого ПРО марсиан
и упавшего, как на банкноту**упавший Экзюпери,
на другую планету, в страшно холодный сухой океан?
Так реально погибли из-за стеченья стихий
дорогостоящие американские корабли.
Так мы вглядываемся в марковские цепочки дней
и с вероятностью ноль запятая три
ту катастрофу, которая у нас внутри,
угадываем вовне.
Март 2001, Париж
Примечания:
Клод Шеннон (1916-2001) - американский математик, один из основателей теории информации и основоположников кибернетики.
* В слегка упрощенном виде - одно из основополагающих уравнений теории Шеннона, читается: "Количество информации равно минус сумме марковских вероятностей, умноженных на логарифм вероятности". Из этого уравнения видно, что максимум информации приходится на диапазон вероятности 0,3 - 0,4.
** 50 французских франков
© Анатолий Величко, 2001-2003.
© Сетевая Словесность, 2001-2003.

